Ingeniería para AES. Representación de figuras tridimensionales en el papel

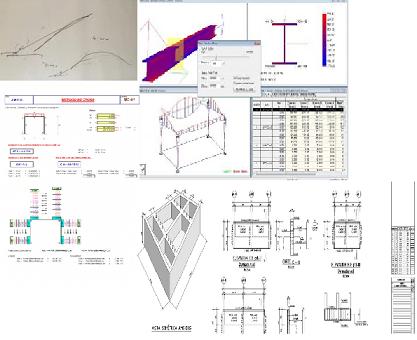
Quizá una de las formas más simples de distinguir a un ingeniero de otras profesiones, es pedirle que dibuje un cubo o un casquete esférico en una hoja de papel. La representación correcta en un espacio de dos dimensiones de una figura tridimensional, incluso tan elemental como éstas, supone conocimientos de dibujo técnico que no forman parte de la formación de muchos.

La vinculación con el papel de los ingenieros es clásica. Pocos podrán sustraerse, si se ven en la necesidad de explicar algo, a dibujar un esquema en una hoja de papel. Puede ser una servilleta, una cuartilla, un trozo de celulosa arrancado a una agenda. La representación gráfica es un medio de expresión consustancial al ingeniero, que suele ser parco en palabras.

Por supuesto, habría que indicar de inmediato que quienes más contacto tienen con la representación, dentro del mundo de las profesiones técnicas, son los arquitectos. Pero hay una diferencia especial entre los dibujos de los arquitectos y los de los ingenieros, relativamente fácil de detectar, incluso para el profano. El arquitecto da más importancia a la línea; el ingeniero concede el mayor valor al concepto que trata de hacer entender.

La afirmación anterior puede despertar la protesta airada de un colectivo respetabilísimo, que se ha acostumbrado, con el paso del tiempo, al trabajo en perfecta cohesión con los ingenieros, que es el de los arquitectos. Si se quiere dar su mérito a los arquitectos, póngase a ambos profesionales a dibujar la proyección de una escalera; el ingeniero apenas si habrá trazado el primer peldaño, mientras que el arquitecto ya estará dibujando las barandillas.

El imperio de la línea en la arquitectura es omnipresente. Uno de los más famosos arquitectos, aún vivo en el momento en que redacto estas líneas, reputado genial diseñador del Centro Cultural de Avilés que lleva su nombre, Niemeyer, lo pergeñó sobre una servilleta de restaurante, pero (y confío en que no me lo desmienta el venerado Oscar Niemeyer) con solo el abocetado de una línea curva.

Otro magnífico arquitecto, Santiago Calatrava, ha ideado bellísimos puentes cuya sustentación es un elemento secundario, algo que resulta difícil de comprender para un ingeniero-tipo. Cito, por último, como un ejemplo más de la distinta liga técnica en la que se diría que militan ambas profesiones, que Rafael Moneo, distinguido como académico de número de la Real Academia de Ingeniería, no había asistido (según la Memoria de Actividades de 2007, que es la que tengo a la vista) a ninguna de las 93 sesiones plenarias que tuvieron lugar desde su fundación. (1)

Los ingenieros han estudiado a fondo múltiples sistemas de representación gráfica (incluidos el sistema cónico y la proyección estereográfica, de aplicación restringida) pero, sobre todo, se han imbuído de métodos de cálculo estructural.

Puede que los hayan olvidado, por falta de práctica, pero han debido superar duros exámenes en los que se les compelía a resolver estructuras, expresión del argot técnico por la que debían deducir, con cuatro datos y unos mallados, momentos y esfuerzos cortantes, flechas, pesos máximos y mínimos sobre vigas, zapatas o forjados, incorporando al papel múltiples resultados y coeficientes misteriosos para el profano que recibían los nombres de tensiones de cizalla, torsores, coeficientes de rigidez, juntas de dilatación, etc.

No pretendo ofrecer un curso rápido de cálculo estructural para abogados y economistas (y, líbreme Dios, aún menos para arquitectos), sino llamar la atención sobre algunas cuestiones relativas a la interpretación de planos, haciendo alusión a los posibles casos que puedan aparecer, eventualmente, sobre la mesa de los profesionales a los que va dirigido este Manual.

La representación más habitual con la que se encontrarán es la de la planta de un piso o chalet. Deberán fijarse, ante todo, en la escala, esto es, la relación entre las dimensiones reales y las representadas. En pocos casos, figurará en el propio plano, con una expresión del tipo 1:50, por ejemplo. Esto quiere decir que 50 decímetros (dm), metros (m) o kilómetros (km) reales se representarán en el plano, respectivamene, como 1 dm, 1 m o 1 km. A partir de ahí, será fácil calcular, en sus dimensiones reales, la superficie del piso, de una habitación o de las zonas comunes.

Una pequeña complicación aparece, sin embargo, debido a la facilidad con la que las fotocopiadoras, incluso las de uso casero, hacen reducciones de planos grandes: Ees muy posible que lo que tenga entre manos sea una reproducción en la que, o bien no esté visible la escala, o esta haya quedado desvirtuada por la fotocopia.

Si esto es así, ha de hacerse la conversión de escalas, realiando pequeños cálculos. Pongamos el caso de que se ha dispuesto originalmente de un plano en dimensión A1 (594x841 mm), en la que todo estaba dibujado a escala 1:100, y se ha hecho la reducción a una hoja de papel A4 (297x210), que es lo que tenemos entre manos. ¿A cuánto equivale ahora 1 cm del dibujo original? (1)

La respuesta inmediata sería: "No tengo ni idea" o "No me interesa lo más mínimo, no voy a comprar ese piso". Pero existen otras, y una es la correcta.

Supongo que el lector conocerá que las dimensiones del papel normalizadas con la letra A están definidas de forma que cada una contiene dos hojas de la siguiente; así la A3 contiene dos A4 y, por tanto, la A1 contiene 8 hojas de A4. Pues bien, la reducción de A1 a A4 es aproximadamente del 35%, puesto que la relación de superficie entre un formato y el inferior es de raiz cuadrada de dos (1/1,414 es decir, el 70,71%) y 70,71*70,71*70,71 (reducción de A1 a A4) es igual a 35,35.

Tenemos, entonces, que 1 cm del plano original a sido reducido a 0,35 (aproximadamente, la figura se ha reducido a una tercera parte)

Para otras conversiones, resulta muy útil la tabla siguiente:

 

fromto	A0	A1	A2	A3	A4	A5	A6	A7	A8	A9	A10
A0	100%	71%	50%	35%	25%	18%	12.5%	8.8%	6.2%	4.4%	3.1%
A1	141%	100%	71%	50%	35%	25%	18%	12.5%	8.8%	6.2%	4.4%
A2	200%	141%	100%	71%	50%	35%	25%	18%	12.5%	8.8%	6.2%
A3	283%	200%	141%	100%	71%	50%	35%	25%	18%	12.5%	8.8%
A4	400%	283%	200%	141%	100%	71%	50%	35%	25%	18%	12.5%
A5	566%	400%	283%	200%	141%	100%	71%	50%	35%	25%	18%
A6	800%	566%	400%	283%	200%	141%	100%	71%	50%	35%	25%
A7	1131%	800%	566%	400%	283%	200%	141%	100%	71%	50%	35%
A8	1600%	1131%	800%	566%	400%	283%	200%	141%	100%	71%	50%
A9	2263%	1600%	1131%	800%	566%	400%	283%	200%	141%	100%	71%
A10	3200%	2263%	1600%	1131%	800%	566%	400%	283%	200%	141%	100%

Si el AES, con estas sencillas explicaciones, no es capaz de entender nada o casi nada, podrá considerarse al mismo nivel de conocimientos en esta materia que un ingeniero típico.

---

(1) Estas aparentemente curiosas dimensiones son debidas a que se eligió como base una hoja rectangular, para el formato A0, tal que tuviera 1 m2 de área y en la que se cumpliera la condición de que la relación entre la altura y la base fuera raiz cuadrada de dos. Esta relación entre los lados del cuadrado (1,4142) se cumple para todos los formatos, que son por tanto, siempre, 141% mayores en superficie que el que tiene el número de orden inmediatamente superior (A3 respecto a A4, por ejemplo) y un 71% más reducidos que el de orden inmediatamente inferior (A2 respecto a A1, por ejemplo).

Naturalmente, aunque estas medidas son las fijadas por la norma ISO existen otras normas que establecen relaciones y medidas distintas, contribuyendo, en mayor o menor medida, a la confusión que genera la especie humana en cualquier sector en el que pretende generar una norma universal.

Nota aclaratoria.- En la figura, en el ángulo superior izquierdo, la servilleta de Niemeyer (o algo parecido). El resto, diversas hojas de cálculo estructural correspondientes al trabajo de empresas proyectistas, formadas, básicamente, por ingenieros calculistas.

(1) Fue, no habría que dudarlo, el único de los Académicos con este comportamiento.