Ingeniería para AES. Transformadas de Laplace y cambio de paradigma

Casi todos los ingenieros -la mayor parte de los vivos y todos los fallecidos en el último cuarto del pasado siglo - han estudiado, en su momento, las transformadas de Laplace. Estas son, con mucho, las más conocidas de las transformadas integrales, lo que no quiere decir que sean muy utilizadas, salvo por los licenciados en matemáticas que trabajan como profesores de alguna asignatura de Cálculo Diferencial.

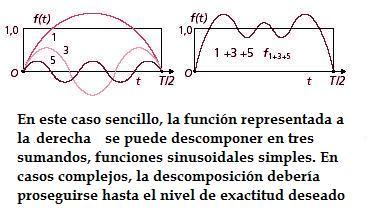
La transformada de Laplace es una generalización de la transformada de Fourier, por la que este insigne matemático demostró que cualquier señal puede transformarse en suma de funciones senoidales, es decir, se puede expresar como una adición de funciones trigonométricas (senos y cosenos). Laplace generalizó esta idea, sustituyendo la variable por números complejos.

La aplicación de las laplacianas tiene un campo inmenso, porque permite resolver ecuaciones diferenciales lineales transformándolas en ecuaciones algebraicas, que son mucho más fáciles de resolver. Por eso, las transformadas de Laplace han demostrado su utilidad para resolver multitud de problemas dinámicos :en los que  es preciso analizar la evolución en el tiempo de cualquier variable.

Muchos problemas prácticos son beneficiarios de esta posibilidad de convertir a operaciones sencillas lo que antes eran ecuaciones diferenciales o integrales muy complejas. Se pueden abordar con estas transformadas cuestiones de conductividad y difusión del calor o del frío, evolución de señales en circuitos electrónicos de funcionamiento sofisticado, o analizar el comportamiento de cuerpos irregulares sometidos a vibraciones y empujes, etc.

El funcionamiento de los intríngulis de las transformadas laplacianas resulta también imprescindible para comprender la problemática inherente a una de las obsesiones actuales de la economía, utilizada frecuentemente por quienes no tienen la menor idea ( o muy poca) acerca de cómo resolver las cuestiones complejas a las que se confrontan, y que pretenden arrumbar proponiendo soluciones etéreas o palabros sin sentido, de las que se ha convertido en recurrente la apelación a que estamos o deberíamos estar, ante un cambio de paradigma.

La propuesta supera, con mucho, lo que está al alcance de un equipo de gobierno, aunque obtenga la mayoría absoluta en las urnas gracias a unas elecciones generales. Esto es así porque, en esencia, un cambio de paradigma consistiría en encontrar una función de transformación que sea asequible para el sistema, esto es, que resulte compatible con las pretensiones de los distintos grupos de presión y realizable económicamente. además (aunque para muchos esto no sea importante) éticamente presentable.

Los cambios de paradigma totales son, por propia definición, y a poco que se considere su dificultad, imposibles.

Las transformadas de Laplace resuelven la forma de modificar una situación inicial, definida por la correspondencia entre un estado de cosas, caracterizado por una función f(x), por medio de un conjunto de operaciones, que caracterizamos por una función L[f(x)] , o un conjunto de relaciones entre los sujetos, expresada mediante ecuaciones L[f(x)]=0, convirtiéndola en una situación diferente, pero con la que guarda unívoca correspondencia.

Para ello, se busca una función transformada F(s) a la que correspondería un  conjunto de operaciones distinto L[F(s)] o un conjunto de ecuaciones, igualmente distinto, L[F(s)]=0, que sea exactamente equivalente, en términos matemáticos , a la original.

Como se puede comprender, un cambio de paradigma no tiene sentido, a no ser que el conjunto de operaciones, L[F(s)], o de ecuaciones transformadas L[F(s)]=0 sea más eficaz, o, en términos matemáticos, sea de análisis y resolución más sencillos, que las operaciones que permitírían encontrar la solución a L[f(x)], o las ecuaciones L[f(x)]=0.

Se ha demostrado que son efectivas, cuando se eligen adecuadamente, las llamadas transformadas integrales, por la que se define la función transformada F(s) como una integral de la función original f(x) multiplicada por alguna función arbitraria de las variables x (antigua) y s (la nueva) que se denomina Núcleo de la transformación.

Pero esto supone que se haya podido expresar como una función, o, al menos, como un conjunto de valores, tanto la función de partida como la objetivo o final.

Existen múltiples reglas de transformación para cambios leves de paradigma. La forma de analizar su viabilidad es comprobar si, en lugar de simplifica el problema, no lo convierten en aún más complejo y, por tanto, hacen la solución inalcanzable.

En la vida real, algunas propuestas de cambio de paradigma -muy queridas por los intuitivos nostálgicos del buenismo o del ecologismo voluntarista- consisten en aconsejar que se abandone cualquier actuación que produzca daño a la naturaleza o a terceros. En su expresión maximalista, esto equivale a reconocerse partidarios de la función de inactividad, por la que, al no hacer nada, no se consigue nada.

Para encontrar las transformadas laplacianas se utilizan ordenadores y, en menor medida, ábacos. Cuando, como sucede en la vida socioeconómica, los problemas son extremadamente complejos, no es posible encontrar la solución que satisfaga a todo el mundo, por lo que cualquier propuesta que provenga de un grupo de opinión o de presión será calificada, sin rubor, pero sin posibilidad de demostrar lo contrario, como falsa o como una elucubración sin sentido por sus opositores.