Ingenieria para Abogados y Economistas. Curvas y curvaturas (2)

Una vez que los ingenieros obtienen su título, prácticamente las únicas curvas que utilizarán el resto de su vida, son siete: la línea recta (que no necesita introducción, aunque el AES debe ser consciente de que toda línea curva puede aproximarse, con la deseada exactitud, a una serie de segmentos rectilíneos), la circunferencia, la parábola (y, en menor medida, las restantes figuras cónicas: elipse e hipérbola), la función de densidad llamada normal (o campana de Gauss), la menos normal función de Poisson, y dos curvas claramente exóticas, la catenaria y la conchoide.

La circunferencia -también llamada círculo, erróneamente, por los no técnicos- es muy importante para referirse a la mayor parte de los objetos industriales cuando se les representa en proyección ortogonal, bien sea en la opción de base o de alzada: tienen esta forma, por ejemplo, las depuradoras -de agua potable como de residual- las bocas de riego, los bordes de los cubos de basura, casi todas las secciones transversales paralelas al terreno, como el corte de una chimenea, un horno de cemento, un horno alto, una bola de billar, un tubo de ensayo, etc-.

La parábola es obtenida al lanzar un pelota de golf, independientemente del hándicap, con tal de que se de a la bola y no solamente al campo. También se pueden ver parábolas en los chorros de las fuentes clásicas (Cibeles o Neptuno, en Madrid), en los faros de automóvil (para desgüace) y en los espejos de las estaciones astrofísicas.  

Mucho más interesantes, porque su uso correcto indica conocimientos que no están al alcance de cualquiera, son las funciones de probabilidad llamadas de Gauss y de Poisson. La primera se obtiene siempre que se repite, y de la misma manera, un número muy grande de veces un experimento apuntando a un resultado concreto.

Esta afirmación necesita, posiblemente, algún comentario adicional. Si halláramos, por ejemplo, el peso medio de todos los niños españoles de cinco años (separados por sexos), la curva que representa el número de niños que tienen un peso dado (distribuído en intervalos, de, digamos, medio kilo) adopta la forma "normal", con una joroba en el medio. 

Los economistas utilizan mucho la distribución normal -sirve, típicamente, para definir el grado de confianza de un sondeo electoral, o para conocer la distribución demográfica por edades o deducir el porcentaje de ancianos que, en un momento determinado, no podrán cobrar la pensión, por ruptura del equilibrio presupuestario de un sistema de jubilaciones-.

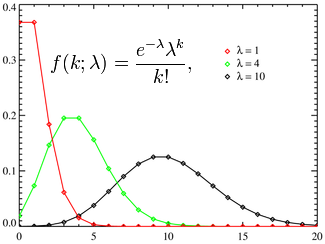
Lo que no suelen aplicar, sin embargo, es la distribución de Poisson, que es, incluso, más normal que la de Gauss, puesto que lo normal es que los sucesos a los que nos confrontamos los seres humanos sean raros.  (1)

Si suponemos, por ejemplo, que solo el 0,02 % de los militantes de un partido saben algo de ingeniería (que ya es un suponer), al elegir 300 alcaldes entre ellos (al azar, que es como suele hacerse), la probabilidad de que 3 de los nombrados tengan alguna idea de ingeniería es P (=3) = e exp (-6) * 6 exp 3/3!, que, efectuadas los cálculos correspondientes, da por resultado final 0,089. Es decir, de cada cien veces que se hagan elecciones, solo 9 se cumplirá esta condición.

Lo que, en una democracia con elecciones cada cuatro años, la verdad es que no resulta muy esperanzador. Aunque también puede contraponerse a esta pesimista idea la interrogante expeditiva de "¿Y para qué necesita un alcalde saber algo de ingeniería, después de todo?", para la que carezco de respuesta equilibrada.

Finalmente, la presentación de la catenaria y la conchoide se encontrará en el Apéndice de este Libro, junto con otros ejemplos -estos ya, en general, imaginarios- de descubrimientos exóticos de los ingenieros para deslumbrar a ingenuos, como el "cajón de los bugilates", "las empinadas pendientes de más de 90º", "la máquina capaz del movimiento continuo" o incluso el "movimiento de inercia ficticio para el cálculo de flechas" en un pilar. Son expresiones parecidas a las de "in vino, veritas", "mater semper certa est sed pater is est quem nuptíae demostrant" o "la gestión privada es siempre más eficiente que la pública".

---

(1) Una función de distribución de Poisson depende de dos valores o parámetros,

en donde k es el número de veces que para el que deseamos saber la probabilidad de que se presente el elemento raro que estamos analizando en un colectivo pequeño y λ representa la proporción de elementos de esa característica en el colectivo general. Por ejemplo, si hay un accidente mortal de automóvil en las carreteras españolas cada día, y estamos interesados en saber la probabilidad de que ocurran k accidentes en 10 días, la respuesta correcta no sería k.10, sino que habrá de usarse el modelo de distribución de Poisson con λ = 10×4 = 40. 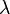(e es la base de los logaritmos naturales: e = 2,718...): f(k;40) = (e (exp-40)*40 expk)/k!.de Poisson está emparentada con la distribución binomial, de la que es su valor límite en condiciones determinadas; también lo está con la función normal, a la que converge (con media nula y desviación típica la unidad), cuando el parámetro   tiene a infinito.